Array Logic and Data-driven Conditionals

Logic and conditions

APL has logical and comparison functions as in-built primitives. Much like the arithmetic, these symbols are like those used in conventional notation.

< ≤ = ≠ ≥ > ∧ ∨ ⍲ ⍱ ~

Some of these are more general mathematical functions which happen to be the same as logical functions when used with Booleans (1s and 0s):

      3 ∧ 4               ⍝ Lowest common multiple

      0 1 0 1 ∧ 0 0 1 1   ⍝ Logical AND

0 0 0 1

      12 ∨ 16             ⍝ Greatest common divisor

      0 1 0 1 ∨ 0 0 1 1   ⍝ Logical OR

0 1 1 1

      'P' ≠ 'Q'           ⍝ Not equal to

      0 1 0 1 ≠ 0 0 1 1   ⍝ Logical XOR

0 1 1 0

Info

The 16 possible logic functions for two binary variables can all be expressed succinctly in APL, as shown in the notebook and webinar on Boolean scans and reductions.

The shape of data

One of the distinguishing features of APL is the multidimensional array. Single elements, lists and tables are quite familiar constructs.

Tables are very useful for representing data which is related in some way. For example, let's say that the price of oranges changes daily. We can represent a week of prices as a 7-element numeric list.

0.35 0.3 0.33 0.32 0.39 0.33 0.36

How about the amount spent on 3 items? We could store this in 3 separate lists, but it is convenient to keep it in a table with 3 rows and 7 columns.

The reshape function ⍺⍴⍵ takes data from ⍵ and uses it to fill out an array of shape ⍺, one row at a time.

      cost ← 3 7⍴4.36 4.22 4.05 4.14 4.18 4.19 4.02 2.79 2.58 2.68 2.77 2.88 2.79 2.52 3.07 3 3.13 3 3.24 3.06 3.29
      cost

4.36 4.22 4.05 4.14 4.18 4.19 4.02
2.79 2.58 2.68 2.77 2.88 2.79 2.52
3.07 3    3.13 3    3.24 3.06 3.29

So what is this table that we have created? In other languages, there are lists, and there are lists of lists. In APL, a list of lists is not the same thing as a table (also known as a matrix). APL arrays contain two essential pieces of information: their shape and their list of elements.

The shape function ⍴⍵ returns the shape of its argument.

      ⍴4 12 31
3

The following table lists the rank (number of dimensions), some common names, and a geometric analogy for the three simplest types of multidimensional arrays.

Rank	Name	Geometric analogy
\(0\)	scalar	point
\(1\)	vector or list	line
\(2\)	matrix or table	rectangle

Arrays with \(3\) or more dimensions are sometimes called cube or cuboid, but they are generally referred to as N-dimensional arrays, rank-N arrays or high rank arrays. Arrays of rank greater than \(3\) are sometimes called noble arrays.

For our cost matrix, the total spent on each item is a row-wise sum:

      +/cost    ⍝ The total cost over the week

29.16 19.01 21.79

      ⍴+/cost   ⍝ For 3 items

The total for each day across all items is a column-wise sum:

      +⌿cost    ⍝ The total cost of 3 items

10.22 9.8 9.86 9.91 10.3 10.04 9.83

      ⍴+⌿cost   ⍝ Over 7 days

Ravel means unravel

Monadic comma is the function ravel ,⍵ and it lays out the elements of an array as a vector, one row at a time — a bit like pulling thread from a spool.

      mat ← 3 3⍴⎕A
      mat

ABC
DEF
GHI

      ,mat

ABCDEFGHI

The outer product

The "outer product" ∘.F operator applies its function operand F between all combinations of elements of its left and right argument arrays.

      F ← {⍺+⍵}
      1 2 3 ∘.F 10 20 30

11 21 31
12 22 32
13 23 33

For example, the catenate function ⍺,⍵ (comma) will join two lists together. We can use the outer product to join combinations of words from two lists.

      1 4 9 , 6 5 4

1 4 9 6 5 4

      'joined up' , 'text vectors'

joined uptext vectors

      'chicken' 'pork' 'vegetable' ∘., ' chow mein' ' with cashew nuts'

┌───────────────────┬──────────────────────────┐
│chicken chow mein  │chicken with cashew nuts  │
├───────────────────┼──────────────────────────┤
│pork chow mein     │pork with cashew nuts     │
├───────────────────┼──────────────────────────┤
│vegetable chow mein│vegetable with cashew nuts│
└───────────────────┴──────────────────────────┘

What are those boxes around the output?

We have just created a nested array. These are arrays in which each element contains another array more complex than a single number or character. The next section on multidimensional and nested arrays introduces them in more detail.

If you do not see lines around the output of the last expression above in your interpreter session, turn boxing on:

      ]box on

Was OFF

      ⍳3 3

┌───┬───┬───┐
│1 1│1 2│1 3│
├───┼───┼───┤
│2 1│2 2│2 3│
├───┼───┼───┤
│3 1│3 2│3 3│
└───┴───┴───┘

Replicate/Compress

The replicate function ⍺/⍵ (yes, some symbols have multiple meanings) repeats elements of an array along rows.

      1 2 3/'ABC'

ABBCCC

      1 2 3/2 3⍴'DYALOG'

DYYAAA
LOOGGG

      1 ¯2 3/2 3⍴'DYALOG'

D  AAA
L  GGG

When used with a Boolean array, the function ⍺/⍵ is called compress.

      0 1 0/2 3⍴'DYALOG'

Y
O

Just like the forward-slash F/ as the reduction operator acts along rows and forward-slash-bar F⌿ reduces down columns*, the replicate ⍺/⍵ and replicate-first ⍺⌿⍵ functions work along different axes of high rank arrays.

*we will see a fuller description when we discuss 3D and higher rank arrays.

Indexing

In many other programming languages, "selection" is used to describe control structures such as "if then else" or "switch case". In APL, we can get a similar effect by literally "selecting" elements from arrays.

Info

Indexing starts from 1 by default. You can change the index origin by setting ⎕IO←0, but this course assumes ⎕IO←1.

      'APPLE'[1 3 4]

APL

      ⍸ 1 0 0 1 0 1

1 4 6

      IsDivisibleBy ← {0=⍵|⍺}
      3 6 8 5 2 IsDivisibleBy 2

0 1 1 0 1

      3 6 8 5 2 {⍺[⍸⍺ IsDivisibleBy ⍵]} 2

6 8 2

Problem set 3

Define the numeric vector nums

nums ← 3 5 8 2 1

Using nums, define mat

mat

3 5 8
2 1 3

Using mat, define wide

      wide

3 5 8 3 5 8
2 1 3 2 1 3

Using mat, define stack

      stack

Answers

```
mat ← 2 3⍴nums
```
```
wide ← mat,mat
```
```
stack ← 2⌿mat
```

Why does 101='101' evaluate to a 3-element list?

Answer

101 is a literal single number (a scalar), whereas '101' is a literal 3-element character vector.

Due to singleton extension, 101='101' compares the single number 101 to each of the 3 characters in the 3-element character vector '101'. The character vector '101' is equivalent to '1' '0' '1' but the number 101 is not the same as the 3-element numeric vector 1 0 1.
Write a function PassFail which takes an array of scores and returns an array of the same shape in which F corresponds to a score less than 40 and P corresponds to a score of 40 or more.
```
      PassFail 35 40 45
```
```
FPP
```
```
      PassFail 2 5⍴89 77 15 49 72 54 25 18 57 53
```
```
PPFPP
PFFPP
```
Answer
```
PassFail ← {'FP'[1+40≤⍵]}
```
This problem is taken from the 2019 APL Problem Solving Competition.

A Grille is a square sheet with holes cut out of it which, when laid on top of a similarly-sized character matrix, reveals a hidden message.

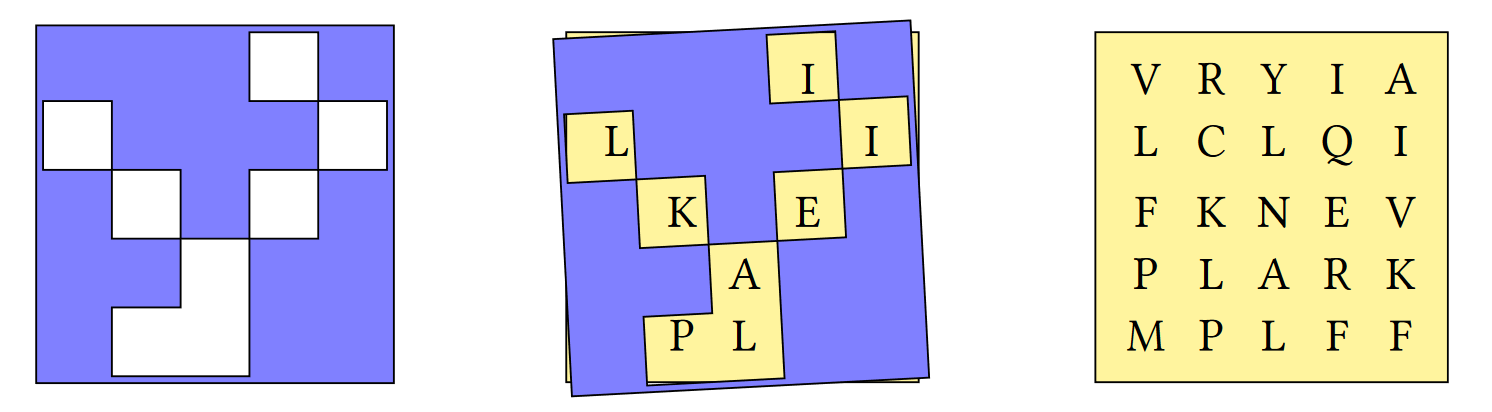
Write an APL function Grille which:
- takes a character matrix left argument where a hash '#' represents opaque material and a space ' ' represents a hole.
- takes a character matrix of the same shape as right argument
- returns the hidden message as a character vector
```
      (2 2⍴'# # ') Grille 2 2⍴'LHOI'
```
```
HI
```
```
      grid   ← 5 5⍴'VRYIALCLQIFKNEVPLARKMPLFF'
      grille ← 5 5⍴'⌺⌺⌺ ⌺ ⌺⌺⌺ ⌺ ⌺ ⌺⌺⌺ ⌺⌺⌺  ⌺⌺'
      grid grille
```
```
┌─────┬─────┐
│VRYIA│⌺⌺⌺ ⌺│
│LCLQI│ ⌺⌺⌺ │
│FKNEV│⌺ ⌺ ⌺│
│PLARK│⌺⌺ ⌺⌺│
│MPLFF│⌺  ⌺⌺│
└─────┴─────┘
```
```
      grille Grille grid
```
```
ILIKEAPL
```
Answer

We can use the where function ⍸⍵ to compute indices of spaces:
```
Grille ← {⍵[⍸⍺=' ']}
```
Or, we can use compress ⍺/⍵ if we first ravel ,⍵ both arguments:
```
Grille ← {(,⍺=' ')/,⍵}
```

Back to School

Write a function to produce the multiplication table from 1 to ⍵.

      MulTable 7

1  2  3  4  5  6  7
2  4  6  8 10 12 14
3  6  9 12 15 18 21
4  8 12 16 20 24 28
5 10 15 20 25 30 35
6 12 18 24 30 36 42
7 14 21 28 35 42 49

Write a function to produce the addition table from 0 to ⍵.

      AddTable 6

0 1 2 3  4  5  6
1 2 3 4  5  6  7
2 3 4 5  6  7  8
3 4 5 6  7  8  9
4 5 6 7  8  9 10
5 6 7 8  9 10 11
6 7 8 9 10 11 12

Answers

```
MulTable ← {(⍳⍵)∘.×⍳⍵}
```
Avoid repeating yourself by assigning values to a name (nums in this example):
```
MulTable ← {nums ∘.× nums ← ⍳⍵}
```
Or, if left and right arguments to a dyadic function are the same, use a selfie F⍨⍵:
```
MulTable ← {∘.×⍨⍳⍵}
```

Using the same three styles as described in part (a) above:

AddTable ← {(¯1+⍳1+⍵)∘.+¯1+⍳1+⍵}
AddTable ← {nums∘.+nums←¯1+⍳1+⍵}
AddTable ← {∘.+⍨¯1+⍳1+⍵}

Making the Grade

Score Range 0-64 65-69 70-79 80-89 90-100

Letter Grade F D C B A

Write a function that, given an array of integer test scores in the inclusive range 0 to 100, returns a list of letter grades according to the table above.
```
      Grade 0 10 75 78 85
```
```
FFCCB
```
Answer

Use an outer product to compare between lower bounds and the scores. The column-wise sum then tells us which "bin" each score belongs to:
```
Grade ← {'FDCBA'[+⌿0 65 70 80 90∘.≤⍵]}
```
You can use a different comparison if you choose to use upper bounds:
```
{'ABCDF'[+⌿64 69 79 89 100∘.≥⍵]}
```
Analysing text
1. Write a function test if there are any vowels 'aeiou' in text vector ⍵
```
      AnyVowels 'this text is made of characters'
1
      AnyVowels 'bgxkz'
0
```
2. Write a function to count the number of vowels in its character vector argument ⍵
```
      CountVowels 'this text is made of characters'
```
```
9
```
```
      CountVowels 'we have twelve vowels in this sentence'
```
```
12
```
3. Write a function to remove the vowels from its argument
```
      RemoveVowels 'this text is made of characters'
ths txt s md f chrctrs
```
Answers
1. With two or-reductions, we ask "are there any 1s in each row?" Then, "are there any 1s in any of the rows?"
```
AnyVowels ← {∨/∨/'aeiou'∘.=⍵}
```
  Or we can ravel the contents of the array into a vector to perform one big or-reduction across all elements:
```
AnyVowels ← {∨/,'aeiou'∘.=⍵}
```
2. Similar techniques can be used for counting the ones:
```
CountVowels ← {+/+/'aeiou'∘.=⍵}
CountVowels ← {+/,'aeiou'∘.=⍵}
```
  Because we are comparing a single vector, +⌿ and ∨⌿ both tell us if there is any vowel in that position:
```
CountVowels ← {+/+⌿'aeiou'∘.=⍵}
CountVowels ← {+/∨⌿'aeiou'∘.=⍵}
```
3. To remove vowels, we must consider the columns of our outer product equality. We then keep elements which are not ~⍵ vowels.
```
RemoveVowels ← {⍵/⍨~∨⌿'aeiou'∘.=⍵}
```
  Or rows if the arguments to our outer product are swapped:
```
RemoveVowels ← {⍵/⍨~∨/'aeiou'∘.=⍵}
```
  Since we are compressing elements out of a vector, we can use either replicate ⍺/⍵ or replicate-first ⍺⌿⍵. This is because a vector only has a single dimension, or axis, and that axis is both the first and the last.
```
RemoveVowels ← {⍵/⍨∨⌿'aeiou'∘.=⍵}
RemoveVowels ← {⍵⌿⍨∨⌿'aeiou'∘.=⍵}
```
Matching shapes
1. Write a function to add a vector ⍵ to each row of a matrix ⍺:
```
      (3 2⍴1 100) AddRows 1 9
2 109
2 109
2 109
      (5 3⍴1 10 100 1000) AddRows 5 10 15
6   20  115
1005   11   25
105 1010   16
15  110 1015
6   20  115
```
2. Write a function to add a vector to each row of a matrix, regardless of the order in which they are supplied:
```
      1 9 AddRows 3 2⍴1 100
2 109
2 109
2 109
      (2 2⍴1 9 11 18) AddRows 9 1
10 10
20 19
```
Answers
1. Reshape recycles elements. We can use this to duplicate rows until we have the correct shape to allow + to map between elements for us:
```
AddRows ← {⍵+(⍴⍵)⍴⍺}
```
2. Finding the maximum shape is a more general solution:
```
AddRows ← {s←(⍴⍺)⌈⍴⍵ ⋄ (s⍴⍺)+s⍴⍵}
```
  This way of applying functions between arrays of different shapes is very common. As with many things in this course, eventually we will discover more elegant methods. Here is an example of using the rank operator:
```
AddRows ← +⍤1
```

These are the heights of some students in 3 classes.

student ← 10 7⍴'Kane   Jonah  JessicaPadma  Katie  CharlieAmil   David  Zara   Filipa '
class ← 'CBACCCBBAB'
height ← 167 177 171 176 178 164 177 177 173 160

Use APL to:

Find the height of the tallest student
Find the name of the tallest student
Find the class to which the tallest student belongs
Find the average height of students in class B

Answers

```
      ⌈/height
178
```

      (height=⌈/height)⌿student
Katie

```
      (height=⌈/height)⌿class
C
```
You might have tried to use indexing and gotten an error:
```
RANK ERROR
        student[⍸height=⌈/height]
                ∧
```
There is additional syntax in order to select from matrices and higher rank arrays.

We can use either compress or indexing to select from the height vector:

      Mean ← {(+/⍵)÷≢⍵}
      Mean (class='B')/height
172.75
      Mean height[⍸class='B']
172.75

Optimus Prime

A prime number is a positive whole number greater than \(1\) which can be divided only by itself and \(1\) with no remainder.

Write a dfn which returns all of the prime numbers between 1 and ⍵.
```
      Primes 10
```
```
2 3 5 7
```
```
      Primes 30
```
```
2 3 5 7 11 13 17 19 23 29
```
Answer
```
Primes ← {⍸2=+⌿0=∘.|⍨⍳⍵}
```
An alternative coding uses the multiplication table:
```
Primes ← {i~∘.×⍨i←1↓⍳⍵}
```
Of course, the outer product ∘.F indicates that the number of calculations to compute both of these solutions increases with the square of the input size. We say they have a computational complexity "of order n squared" or \(O(n^2)\) in big-O notation. This is a very inefficient way to find prime numbers. To see discussions around more efficient ways to compute prime numbers in APL, see the dfns page on prime numbers.

Score Range	`0-64`	`65-69`	`70-79`	`80-89`	`90-100`
Letter Grade	F	D	C	B	A